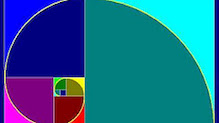
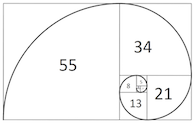
Klik in bovenstaand plaatje. In dit korte filmpje op Youtube kun je zien hoe De gulden rechthoek wordt gemaakt door de getallenreeks van Fibonacci en hoe je door de diagonalen van de vierkanten bogen kunt tekenen, die met elkaar verbonden een mooie spiraal vormen. Kijk ook naar het rechter plaatje en lees over:
De reeks van Fibonacci
Leonardo van Pisa ook wel bekend als Fibonacci beschreef een bijzondere rij getallen in zijn boek Liber Abaci in het jaar 1202, hoewel in latere studies bleek dat deze reeks ook al eerder bekend was bij Indiase en Arabische wiskundigen. Ook wordt de reeks in verband gebracht met De gulden snede (zie onder):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,.. zie de rechterkolom voor de eerste 200 getallen van deze reeks.
Men laat de rij ook wel met 1 en 1 beginnen in plaats van met 0 en 1. Elk element is afkomstig van de som van de vorige twee elementen. Bijvoorbeeld, het getal 13 wordt verkregen door de getallen 5 en 8 bij elkaar op te tellen en het getal 21 wordt verkregen door 8 bij 13 op te tellen. Hiermee beschrijft de rij van Fibonacci een groeipatroon. Dit wordt duidelijk als men de reeks ruimtelijk gaat uitbeelden.
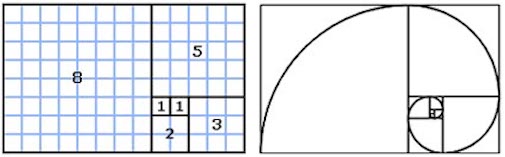
Zie onderstaande tekening:
Het getal 1 staat voor een vierkant van 1 bij 1 en het getal 2 voor een vierkant van 2 bij 2. Als men de zijden van het vierkant 1 bij 1 optelt bij het vierkant 2 bij 2 krijgt men de zijde van het volgende vierkant dat 3 bij 3 groot is. Dit kan men herhalen tot in de oneindigheid en bij elke stap wordt het vierkant groter.
Wanneer men een gebogen lijn door de hoekpunten van de vierkanten tekent, ontstaat een spiraal.
Deze spiraal is in de natuur te vinden, bijvoorbeeld in een slakkenhuis, in het hart van een zonnebloem, in de schikking van bloemblaadjes, in het oog van een orkaan, of in draaiende melkwegstelsels.
De gulden snede in de natuur
De gulden hoek (ongeveer 137,5°) is de hoek die een cirkel volgens De gulden snede verdeelt. In de natuur zien we die hoek terug in delen van bloemen zoals bloemblaadjes, zaden en kelkbladeren.
Om optimaal zonlicht te kunnen opvangen is het belangrijk dat de blaadjes allemaal een andere kant op groeien
en zo een schijf vormen. Als elk blaadje een gulden hoek met zijn voorganger vormt, wordt de schijf het meest efficiënt gevuld. Wanneer je dit vergelijkt met bijvoorbeeld een hoek van 120°, dan groeit het vierde blaadje in dat geval op precies dezelfde plek als het eerste blaadje, het zevende ook, enzovoort. Er ontstaan dan drie pakketjes van over elkaar heen groeiende blaadjes, op 0°, 120° en 240°.

De knoppen van de buisbloempjes van de zonnebloem zijn op het bloembed geordend in Fibonacci-spiralen, 34 naar links en 55 naar rechts; twee getallen uit de rij van Fibonacci. Bron: - Own work
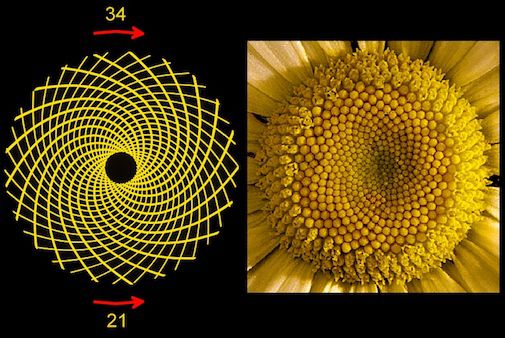
Bron: http://britton.disted.camosun.bc.ca/fibslide/fib31.gif
Fibonaccigetallen in de natuur: http://britton.disted.camosun.bc.ca/fibslide/jbfibslide.htm
De Bloem van de eenstijlige Meidoorn (Crataegus Monogyna) in Lichttuin heeft 5 blaadjes, een Fibonaccigetal.
Bron: https://fibspiral.files.wordpress.com

Bron: http://www.phys.tue.nl/TULO/guldensnede/rechthoek.html
De gulden snede en Het gulden getal
Het gulden getal wordt ook wel ‘goddelijke verhouding’ of ‘gulden snede’ genoemd. Het wordt weergegeven door de Griekse letter φ (Phi), als eerbetoon aan de beeldhouwer en architect Phidias (ca. 490-431 v. C.)
Phi is ongeveer 1,61803398874989...
Onder de Grieken was het getal al bekend; het werd gebruikt in de architectuur om de verhoudingen vast te leggen van beelden en tempels, zowel van de plattegrond als van de gevels. Een goed voorbeeld is het Parthenon van Phidias.
Verhandelingen over De gulden snede komen we aanvankelijk alleen op wiskundig gebied tegen. De eerste zou geschreven zijn door Theano, een arts en wiskundige die tot de school van Pythagoras behoorde. Maar dit werk zou verloren zijn geraakt.
Euclides was een van de eersten die het getal beschreef als de verhouding van twee lijnstukken a en b die voldoen aan de formule (a+b)/a=a/b (uit het Boek der oneindigheid)
De gulden snede, ook wel de verdeling in uiterste en middelste reden genaamd, is de verdeling van een lijnstuk in twee delen in een speciale verhouding. Bij De gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste deel aan met a en het kleinste deel met b, dan is de verhouding van beide zo dat a : b = (a+b) : a.
Euclides' verhandeling over het onderwerp werd in 1509 aan de vergetelheid ontrukt door de Italiaan Luca Pacioli. In De Divina Proportione noemt deze De gulden snede de "goddelijke verhouding".
De gulden snede werd veel gebruikt in de renaissance, met name in de kunst en de architectuur. Hij werd gezien als de perfecte verhouding tussen de zijden van een rechthoek, die De gulden rechthoek (zie onder voor de constructie van zo'n rechthoek) heette en is terug te vinden in de grote werken van Leonardo da Vinci (1452-1519), die belangstelling had voor de wiskunde van kunst en natuur.
Het tekenen van een gulden rechthoek
Een gulden rechthoek, onderverdeeld in een vierkant en een kleinere gulden rechthoek, met zijden
in de verhouding van het gulden getal: lengte : breedte = φ.
Aangetoond kan worden dat φ (phi) ongeveer 1,618 is.
Constructie met passer en liniaal
Bij de vorige constructie was de lengte van het lijnstuk bekend: AB (we gaven dit de lengte 2).
In de figuur is de lengte van het langste deel bekend en ook deze geven we de lengte 2.

Teken een vierkant van 2 x 2, verdeel de basis in 2 gelijke delen
en trek van hieruit een diagonaal naar een hoekpunt.
Cirkel nu deze diagonaal vanaf het middelpunt E om naar het verlengde van de basis: snijpunt F.
Punt D is nu De gulden snede van lijnstuk AF en de formule wordt dus:AF : AD = AD : DF
Cirkel nu deze diagonaal vanaf het middelpunt E om naar het verlengde van de basis: snijpunt F.
Punt D is nu De gulden snede van lijnstuk AF en de formule wordt dus:AF : AD = AD : DF
√5 is hier door EC gevormd, met de stelling van Pythagoras: ED2 + DC2 = EC2
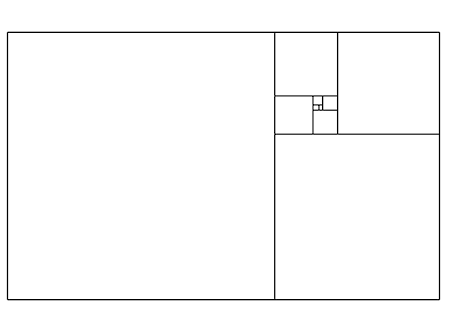
Als we in De gulden rechthoek een vierkant tekenen, met a als zijde, is de kleinere rechthoek die overblijft opnieuw een gulden rechthoek. Door dit proces met de steeds kleiner wordende rechthoeken te herhalen ontstaat een gulden spiraal, ook wel Fibonacci-spiraal genoemd, naar de rij van Fibonacci.
Meer over De gulden snede
De vier lengtes in dit symbool (aangegeven met verschillende kleuren) verhouden zich tot elkaar als De gulden snede.
Johannes Kepler beschreef De gulden snede als een "kostbaar juweel": "De meetkunde heeft twee grote schatten: de ene is de stelling van Pythagoras, en de andere de verdeling van een lijn in extreme en gemiddelde ratio; de eerste kunnen we vergelijken met een hoeveelheid goud, de tweede mogen we een kostbaar juweel noemen."
Martin Ohm wordt verondersteld de eerste te zijn die de term gulden snede gebruikte om deze verhouding te beschrijven. Hij deed dat omstreeks 1830.
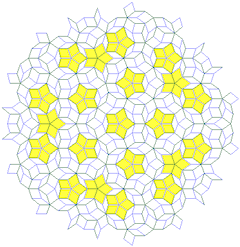
Roger Penrose ontdekte een patroon (de Penrose-betegeling) dat De gulden snede gebruikt in het veld van niet-periodieke vlakvullingen. Dit leidde tot nieuwe inzichten in quasikristallen:
Esthetica
Het duurde tot de 19e eeuw voordat De gulden snede buiten het domein van de wiskunde een bijzondere betekenis werd toegekend.
De gulden snede zou sindsdien volgens sommigen een intrinsieke schoonheid bezitten waardoor die verhouding veel zou voorkomen in klassieke architectuur en schilderkunst. Ook de beelden die Phidias maakte in het Parthenon worden door sommigen in verband gebracht met De gulden snede. De eerste letter van zijn naam, de Griekse letter φ, werd daarom door Mark Barr gebruikt om De gulden snede aan te duiden.
De esthetische status van De gulden snede blijft omstreden. Eerder dan ca. 1830 komt De gulden snede niet voor in geschriften over schilderkunst of architectuur en voor de bewering dat de verhouding vaak zou voorkomen of dat de mens een onbewuste voorkeur voor deze verhouding zou hebben, bestaat geen statistisch bewijs. In de loop van de twintigste eeuw verwierf De gulden snede niettemin een plaats in diverse vormen van kunstonderwijs.
Omdat De gulden snede zo veelvuldig voorkomt in de natuur (zie ook de rij van Fibonacci) zijn we er als mens erg vertrouwd mee. Het is voor onze onderbewuste zintuiglijke verwerking sneller te begrijpen dan wanneer een verhouding niet voldoet aan De gulden snede. Hierdoor is het aannemelijk dat dit universeel als esthetisch wordt ervaren.
Fibonaccigetallen in bloemen
 1
1 3
 5
5
 8
8
 13
13
 21
21
 34
34
http://britton.disted.camosun.bc.ca/fibslide/jbfibslide.htm

Links
De eerste 200 Fibonaccigetallen
F0 + F1 = F2;
F1 + F2 = F3;
F2 + F3 = F4;
F3 + F4 = F5;
enz.
F0
0
F1
1
F2
1
F3
2
F4
3
F5
5
F6
8
F7
13
F8
21
F9
34
F10
55
F11
89
F12
144
F13
233
F14
377
F15
610
F16
987
F17
1597
F18
2584
F19
4181
F20
6765
F21
10946
F22
17711
F23
28657
F24
46368
F25
75025
F26
121393
F27
196418
F28
317811
F29
514229
F30
832040
F31
1346269
F32
2178309
F33
3524578
F34
5702887
F35
9227465
F36
14930352
F37
24157817
F38
39088169
F39
63245986
F40
102334155
F41
165580141
F42
267914296
F43
433494437
F44
701408733
F45
1134903170
F46
1836311903
F47
2971215073
F48
4807526976
F49
7778742049
F50
12586269025
F51
20365011074
F52
32951280099
F53
53316291173
F54
86267571272
F55
139583862445
F56
225851433717
F57
365435296162
F58
591286729879
F59
956722026041
F60
1548008755920
F61
2504730781961
F62
4052739537881
F63
6557470319842
F64
10610209857723
F65
17167680177565
F66
27777890035288
F67
44945570212853
F68
72723460248141
F69
117669030460994
F70
190392490709135
F71
308061521170129
F72
498454011879264
F73
806515533049393
F74
1304969544928657
F75
2111485077978050
F76
3416454622906707
F77
5527939700884757
F78
8944394323791464
F79
14472334024676221
F80
23416728348467685
F81
37889062373143906
F82
61305790721611591
F83
99194853094755497
F84
160500643816367088
F85
259695496911122585
F86
420196140727489673
F87
679891637638612258
F88
1100087778366101931
F89
1779979416004714189
F90
2880067194370816120
F91
4660046610375530309
F92
7540113804746346429
F93
12200160415121876738
F94
19740274219868223167
F95
31940434634990099905
F96
51680708854858323072
F97
83621143489848422977
F98
135301852344706746049
F99
218922995834555169026
F100
354224848179261915075
F101
573147844013817084101
F102
927372692193078999176
F103
1500520536206896083277
F104
2427893228399975082453
F105
3928413764606871165730
F106
6356306993006846248183
F107
10284720757613717413913
F108
16641027750620563662096
F109
26925748508234281076009
F110
43566776258854844738105
F111
70492524767089125814114
F112
114059301025943970552219
F113
184551825793033096366333
F114
298611126818977066918552
F115
483162952612010163284885
F116
781774079430987230203437
F117
1264937032042997393488322
F118
2046711111473984623691759
F119
3311648143516982017180081
F120
5358359254990966640871840
F121
8670007398507948658051921
F122
14028366653498915298923761
F123
22698374052006863956975682
F124
36726740705505779255899443
F125
59425114757512643212875125
F126
96151855463018422468774568
F127
155576970220531065681649693
F128
251728825683549488150424261
F129
407305795904080553832073954
F130
659034621587630041982498215
F131
1066340417491710595814572169
F132
1725375039079340637797070384
F133
2791715456571051233611642553
F134
4517090495650391871408712937
F135
7308805952221443105020355490
F136
11825896447871834976429068427
F137
19134702400093278081449423917
F138
30960598847965113057878492344
F139
50095301248058391139327916261
F140
81055900096023504197206408605
F141
131151201344081895336534324866
F142
212207101440105399533740733471
F143
343358302784187294870275058337
F144
555565404224292694404015791808
F145
898923707008479989274290850145
F146
1454489111232772683678306641953
F147
2353412818241252672952597492098
F148
3807901929474025356630904134051
F149
6161314747715278029583501626149
F150
9969216677189303386214405760200
F151
16130531424904581415797907386349
F152
26099748102093884802012313146549
F153
42230279526998466217810220532898
F154
68330027629092351019822533679447
F155
110560307156090817237632754212345
F156
178890334785183168257455287891792
F157
289450641941273985495088042104137
F158
468340976726457153752543329995929
F159
757791618667731139247631372100066
F160
1226132595394188293000174702095995
F161
1983924214061919432247806074196061
F162
3210056809456107725247980776292056
F163
5193981023518027157495786850488117
F164
8404037832974134882743767626780173
F165
13598018856492162040239554477268290
F166
22002056689466296922983322104048463
F167
35600075545958458963222876581316753
F168
57602132235424755886206198685365216
F169
93202207781383214849429075266681969
F170
150804340016807970735635273952047185
F171
244006547798191185585064349218729154
F172
394810887814999156320699623170776339
F173
638817435613190341905763972389505493
F174
1033628323428189498226463595560281832
F175
1672445759041379840132227567949787325
F176
2706074082469569338358691163510069157
F177
4378519841510949178490918731459856482
F178
7084593923980518516849609894969925639
F179
11463113765491467695340528626429782121
F180
18547707689471986212190138521399707760
F181
30010821454963453907530667147829489881
F182
48558529144435440119720805669229197641
F183
78569350599398894027251472817058687522
F184
127127879743834334146972278486287885163
F185
205697230343233228174223751303346572685
F186
332825110087067562321196029789634457848
F187
538522340430300790495419781092981030533
F188
871347450517368352816615810882615488381
F189
1409869790947669143312035591975596518914
F190
2281217241465037496128651402858212007295
F191
3691087032412706639440686994833808526209
F192
5972304273877744135569338397692020533504
F193
9663391306290450775010025392525829059713
F194
15635695580168194910579363790217849593217
F195
25299086886458645685589389182743678652930
F196
40934782466626840596168752972961528246147
F197
66233869353085486281758142155705206899077
F198
107168651819712326877926895128666735145224
F199
173402521172797813159685037284371942044301
F200
280571172992510140037611932413038677189525